Asal Sayılar Kriptografide Neden ve Nasıl Kullanılır?

Günümüzde çok önemli bir yer tutarak verilerin güvenliğini sağlayan kriptografi alanında büyük asal sayılar çeşitli şifreleme protokollerini oluşturmada önemli rol oynar. Yaygın olarak kullanılan birçok şifreleme algoritmalarının güvenliği, büyük sayıları asal bileşenlerine ayırma zorluğuna dayanır. Özellikle internet üzerinde güvenli iletişimin ayrılmaz bir parçası olan ve yaygın olarak benimsenen RSA algoritması, genel ve özel anahtarları oluşturmak için büyük asal sayıları kullanır.

 

Asal Sayılar ve Kriptografi

 

RSA ve diğer genel anahtarlı şifreleme sistemlerinin güvenlik gücü, kullanılan asal sayıların boyutu ile doğrudan ilişkilidir. Daha büyük asal sayılar, saldırganların şifreyi çözmesini çok daha zor hale getirir. Bu sistemler, büyük asal sayıların çarpanlarına ayrılmasındaki asimetriye dayanır. Yani, iki büyük asal sayıyı çarpmak kolayken, bu sayıları çarpanlarına ayırmak hesaplama açısından zordur. Şu anda, bu büyük sayıları etkili bir şekilde çarpanlarına ayırmak için bir çözüm olmadığı bilinmektedir. Kriptografide şifrelerin geri çözülememesi için tersinemez (veya tersinmesi zor) fonksiyonlar önemli yer taşır ve büyük asal sayıların çarpanlarına ayrılması da kolay olmadığından asal sayılar bizim için çok önemlidir.

 

Peki şifrelemede kullanacağımız büyük bir sayının asal olup olmadığını nasıl kontrol edebiliriz? Bunun için tarih boyunca çeşitli yöntemler geliştirilmiştir. Bunlardan iki tanesine örnek olarak Miller-Rabin Testi ve Eratosthenes Eleği’ni sayabiliriz. Bu iki asallık testine geçmeden önce yazının başından beri sıklıkla bahsettiğim RSA hakkında bilgi vermek istiyorum.

 

RSA Nedir?

 

RSA asimetrik bir şifreleme yöntemidir. Yani public key’in yanı sıra private key de kullanır. İsmini bu yöntemi bulanların baş harflerinden almaktadır (Rivest, Adi Shamir, Leonard Adleman).

 

RSA'da bir kullanıcı, public key (herkes tarafından erişilebilirdir) ve private key (gizli kalmak zorundadır) olmak üzere bir çift anahtar kullanır. Sistemin güvenliği, büyük bir tam sayı içeren public key’e sahip olunsa bile bu sayının asal çarpanlarını içeren private key’e ulaşılmasının bilgisayar açısından makul bir zamanda olanaksız olması gerçeğine dayanır. Özellikle büyük asal sayı tercihi, güvenliği daha da artıracaktır.

 

Bu şifreleme yöntemi aşağıdaki adımları takip eder:

 

1. 2 tane asal sayı (p ve q) seçilir. Bu asal sayıların büyük olması gerekir.
2. “n = pq” olmak üzere n sayısı belirlenir. Bu sayı public sayıdır.
3. (n) = (p) (q) = (p-1)(q-1)
   1. Burada n sayısının Euler totient fonksiyonu hesaplanır. Bu fonksiyon, girdi olarak verilen sayının kendinden küçük 0’dan büyük kaç tane aralarında asal olduğu sayı var onun bilgisini verir.
   2. p sayısı halihazırda asal olduğu için kendinden küçük tüm sayılarla aralarında asaldır. Aynı şekilde q sayısı da öyledir.
4. 1 < e < (n)
   1. Eşitsizliğini sağlayan bir e sayısı seçeriz. Buradaki e bizim public keyimizdir.
5. de = 1 mod((n))
   1. Olmak üzere bir d sayısı seçeriz. Buradaki d bizim private keyimizdir.
6. c = me modn
7. m = cd modn

 

Buradaki zorluk kriptografideki ayrık logaritma problemine dayanır. Üssü hesaplamak oldukça zordur ve key’in bilinmesi gerekir.

 

Buradaki problemi ve neden hesaplamanın oldukça zor olduğunu anlamak için “Diffie-Hellman key exchange” konusunu öğrenmek çok yerinde olacaktır. Bunun için Alice ve Bob isimlerinde iki kişinin haberleşmek istediklerini varsayalım. Bu durumda mesajları şifrelemek için ortak bir anahtar kullanmak istiyorlarsa, bu anahtarın her ikisinde de bulunması gerekir ancak bu anahtarı da açık olarak göndermek doğru olmaz.

 

Aşağıda bu durum için bir şema görebilirsiniz. Algoritma, şema üzerinde daha anlaşılır olacaktır:

 

 

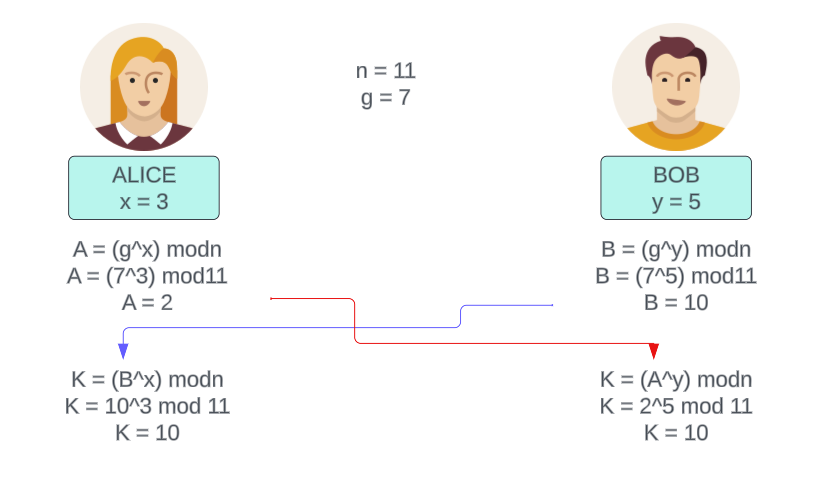
n ve g public olarak belirlediğimiz 2 büyük asal sayımız.

 

x Alice’in, y ise Bob’ın private sayısı.

 

Ayrık logaritma problemi sayesinde saldırgan private key olmadan şifreleri öğrenemez. Bu bize anahtar değişiminde güvenli bir algoritma sunar.

 

MILLER-RABIN: Büyük Asal Sayı Testi İçin Güçlü Bir Algoritma

 

Bahsettiğimiz gibi güvenli şifreleme sistemlerinde kullanmak için büyük asal sayıların etkili bir şekilde bulunması gerekiyor. Bu noktada karşımıza çıkan zorluklardan biri büyük sayıların asallığını kontrol etmenin hesaplama açısından zorluğudur. Miller-Rabin Testi, bu zorluğu aşmak için kullanılan olasılık temelli bir testtir. Michael Oser Rabin ve Gary Lee Miller tarafından geliştirilmiştir. Algoritma ile bir sayının asal olup olmadığı anlaşılır.

 

Miller-Rabin asallık testinde, asal değerler için geçerli olduğu bilinen belirli bir özelliğin, test edilen sayı için geçerli olup olmadığını kontrol ederiz. Eğer test “bu sayı asaldır” diyorsa aslında bu “bu sayı muhtemelen asaldır” anlamına gelir. Ancak testi yaparsak ve sayının asal olmadığı söylenirse, bu sayının asal olmadığından %100 emin oluruz.

 

Başlangıçta sayının asal olduğunu varsayarız. Eğer yanlış bir ifadeye ulaşırsak bu, başlangıçtaki varsayımımızın yanlış olduğu anlamına gelir. Yani sayımız asal değildir.

 

Miller-Rabin testinin adımları:

 

1. n-1 = 2km
   1. n: test ettiğimiz sayı
   2. k, m tam sayılar
2. Yandaki eşitliği sağlayacak bir a sayısı seçilmelidir: 1 < a < n-1
3. b₀ = am(mod n), bi = bi-12(mod n)

 

Örnek: 53 asal mıdır?

 

1. n-1 = 2^km
   1. n = 53
   2. 52 = 2^km
      1. 52/2¹ = 26
      2. 52/2² = 13
      3. 52/2³ = 6.5
      4. 6.5 tam sayı olmadığından burada dururuz
      5. En son tam sayı üs olan 2’yi k olarak(2²), ve m’yi de sonuç olan 13 olarak alırız.
   3. 52 = 2².13
      1. k = 2
      2. m = 13
2. 1 < a < n-1
   1. 1 < a < 52
   2. a = 2 (Ne seçildiği fark etmez ancak küçük sayı seçmek daha avantajlıdır.)
3. b₀ = a^m(mod n), b_i = b_i-1²
   1. b0 = 2¹³(mod 53) = 30(mod 53)
   2. Burada b0’ın +1 veya -1’e eşit olup olmadığına bakıyoruz.
   3. Eğer b₀ ikisinden herhangi birine eşitse, sayımız muhtemelen asaldır.
   4. Burada b₀ değerimiz 30. Yani bir sonraki adıma, b1’i hesaplamaya geçmeliyiz.
   5. b1 = b0²(mod53) = -1(mod53)
      1. Yine b1’in +1 veya -1’e eşit olup olmamasına bakarız.
      2. +1 🡪 Sayının asal olmadığı anlamına gelir.
      3. -1 🡪 Sayının muhtemelen asal olduğu anlamına gelir.
         1. Şu anki durum bu, sonuç olarak 53 muhtemelen asaldır diyebiliriz.

 

Miller-Rabin Testi, büyük asal sayıların testi için güçlü bir araçtır. Asallık testlerinin karmaşıklığını ve hesaplama maliyetini azaltarak, kriptografik uygulamalarda kullanılan büyük asal sayıların etkili bir şekilde seçilmesine yardımcı olur. Ancak, kesinlikle asal olup olmadıklarını belirleme konusunda mutlak bir güvence sağlamaz. Bu nedenle, genellikle Miller-Rabin testinin diğer asal sayı testleri ve algoritmalarla birlikte kullanılması tercih edilir.

 

Bu testin kod olarak örneğini de aşağıda görebilirsiniz:

 

 

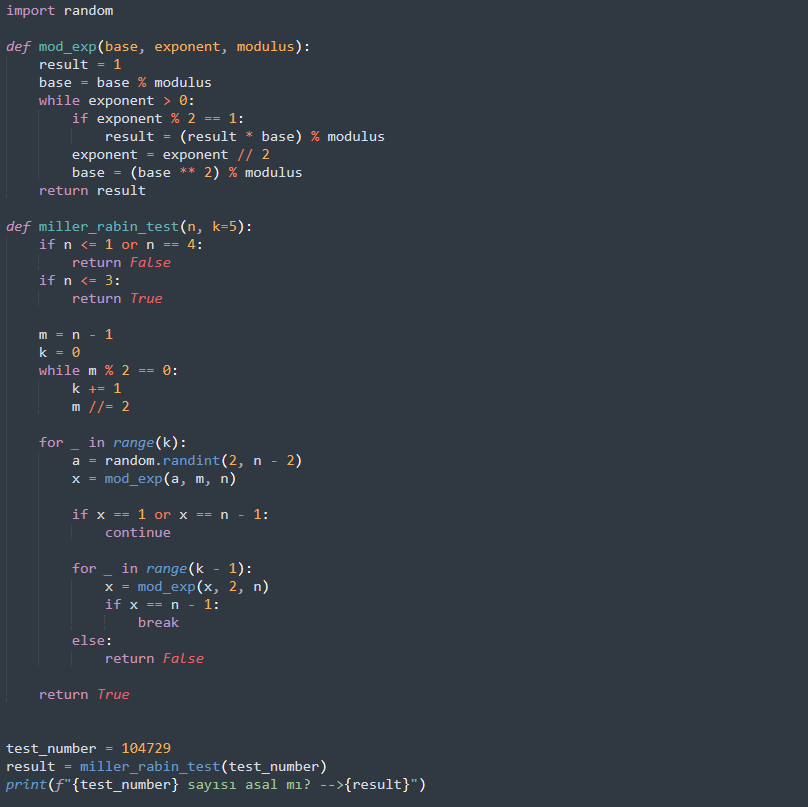
Eratosthenes’in Eleği

 

En basit ve en eski asallık testlerinden biridir. Milattan önce 200’lü yıllarda Antik Yunan’da yaşayan Eratosthenes tarafından geliştirilmiştir. İsminden de anlaşılacağı üzere test, bir elek gibi davranarak asal olmayan sayıları eler ve elimizde asal sayılar kalır.

 

Bu test ile belirlenen bir sayıya kadar olan tüm asal sayılar listelenebilir.

 

Örneğin:

 

• 100’e kadar olan tüm asal sayıları listeleyelim. Öncelikle 2-100 arasındaki sayıları içeren bir tablo oluştururuz.
• Adımlar:
  • 2’yi asal olarak işaretleriz.
  • 2’yi asal olarak işaretledikten sonra 2’nin tüm katlarını asal değil olarak işaretleriz çünkü bu sayılar 1 ve kendileri dışında 2’ye de bölünebilirlerdir.
  • Sıradaki sayı olan 3’ü asal olarak işaretleriz.
  • Aynı şekilde 3’ün katlarını da asal değil olarak işaretleriz.
  • Sıradaki sayı olan 5’i asal olarak işaretleriz.
  • Aynı şekilde 5’in katlarını da asal değil olarak işaretleriz.
  • Sıradaki sayı olan 7’yi asal olarak işaretleriz.
  • Aynı şekilde 7’nin katlarını da asal değil olarak işaretleriz.
  • Buraya kadar geldiğimizde 8, 9, 10 işaretlenmiş olur.

 

Görüldüğü üzere tabloda bir bir ilerlerken asal değil olarak işaretlediğimiz sayıları atlarız. İşaretlenmeyen bir sayı gördüğümüzde o sayı asal demektir.

 

Adımları tamamladığımızda 1’den 100’e kadar işaretlenmemiş sayıları da asal olarak işaretleyebiliriz. Çünkü sonraki sayımız olan 11’i kendisi ile çarptığımızda 100’den büyük bir sayı elde ederiz. Diğer sayılar ile (2, 3, 4, 5, …, 10) çarpmamızın önemi yoktur çünkü zaten o sayıların katlarını önceki adımlarda elemiştik.

 

Eratosthenes’in Eleği, belirli bir aralıktaki asal sayıları hızlı bir şekilde tespit etmek için oldukça etkili bir yöntemdir. Bu algoritma, asal sayıları test etmek için hızlı ve basit bir yaklaşım sunar. Ancak, büyük asal sayıları bulmak için Miller-Rabin gibi diğer algoritmalarla birlikte kullanılarak daha güçlü bir asal sayı testi sağlanabilir.

 

Bu testin kod olarak örneğini de aşağıda görebilirsiniz:

 

 

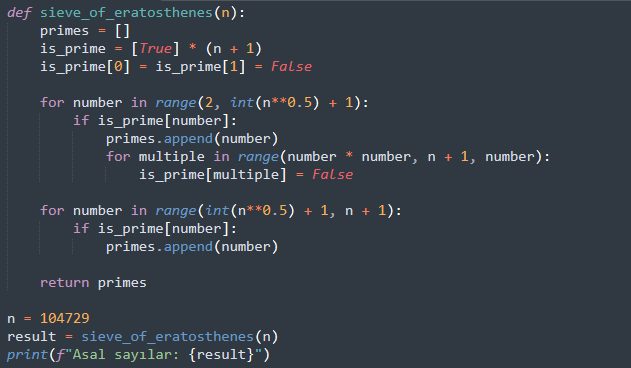
Kriptografide Asal Sayıların Seçimi ve Kullanımı

 

Bu yazıda, kriptografi dünyasının gizemli ve güçlü temsilcileri olarak karşımıza çıkan asal sayıların önemini keşfettik. Asallığın, bilgi güvenliğindeki temel taşlardan biri olarak nasıl işlev gördüğünü ve neden bu kadar değerli olduğunu anladık. Şimdi, kriptografik algoritmaların niçin asal sayıları tercih ettiğini ve bunları nasıl kullandığına bir göz atalım.

 

• Asal sayılar, matematiksel karmaşıklığı ve eşsiz özellikleriyle bilgi güvenliği dünyasında özel bir rol oynar. Şifreleme algoritmaları, bu özellikleri kullanarak güvenli anahtarları oluşturur ve hassas bilgileri korur. Örneğin, RSA algoritması, asal sayıların çarpanları arasındaki özel ilişkileri kullanarak iletişimi şifreler ve iletişimin güvenliğini sağlar.
• Ancak, sadece bu algoritmalar değil aynı zamanda asal sayıları tespit etmek ve doğrulamak için kullanılan testler de kritik öneme sahiptir. Miller-Rabin Testi, büyük asal sayıları etkili bir şekilde sınamak için güçlü bir araçtır. Eratosthenes Eleği, belirli bir aralıktaki asal sayıları hızlı bir şekilde eleme işlemi için kullanılır. Atkin Eleği ise modern bilgisayar sistemlerinde büyük asal sayıları bulmak için optimize edilmiş bir algoritmadır.

 

Bilgi güvenliği, asal sayıların izlediği yoldan ilerler; bu yolda, matematik ve bilgi güvenliği mühendisliğinin birleşiminde, güçlü şifreleme algoritmaları ve güvenli iletişim sistemleri doğar. Gelecekteki siber dünyamızda, asal sayılar bu önemli rolü sürdürmeye devam edecek ve kriptografinin sırları, güvenli bir dijital yaşamın temelini oluşturacaktır.