ÖRNEK 1:
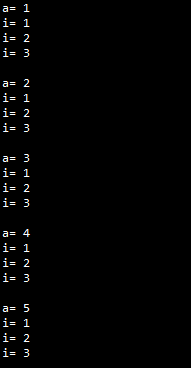
Aşağıdaki programda, dış döngü olan a parametreli döngü 5 kez çalışıyor (a=1, 2, 3, 4, 5). a’nın her değeri içinse içteki döngü 3 kez çalışıyor (i=1, 2, 3). Böylece aşağıdaki çıktı elde ediliyor:
KOD BLOĞU:
public class IcIce
{
public static void main(String args[])
{
int a,i; //5 kez tekrarla
for(a=1;a<=5;a++)
{
System.out.println("a= "+a);
for(i=1;i<=3;i++) //3 kez tekrarla
{
System.out.println("i= "+i);
}
System.out.println();
}
}
}
PROGRAMIN ÇIKTISI:
ÖRNEK 2: ÇARPIM TABLOSU
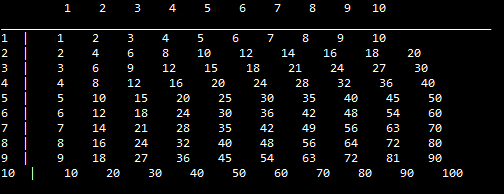
1’den 10’a kadar sayılar için bir çarpım tablosu hazırlamak istiyoruz. Bunun için iç içe 2 döngü yeterlidir ve her iki döngünün de parametresi 1’den 10’a kadar değişecektir. Programın kodu şu şekildedir:
KOD BLOĞU:
public class CarpimTablosu
{
public static void main(String args[])
{
int altcizgi, i, j;
System.out.println(" 1 2 3 4 5 6 7 8 9 10 ");
for(altcizgi=1; altcizgi<=70; altcizgi++) //döngüyle uzunca bir çizgi çizelim
{
System.out.print("_");
}
System.out.println();
for (i =1; i<=10; i++)
{
System.out.print(i+" | ");
for (j=1 ; j<=10 ; j ++)
{
System.out.print(i*j +" ");
}
System.out.println();
}
}
}
PROGRAMIN ÇIKTISI:
ÖRNEK 3: FAKTÖRİYELLİ TERİMLERDEN OLUŞAN SERİ TOPLAMI
Aşağıdaki seri toplamını hesaplayacak bir Java programı yazalım:
1/ 2! + 1/3! + 1/4! +...+ 1/10!
Bu seri toplamını hesaplamak istediğimizde, iç içe iki döngü kullanmak gerektiğini hemen anlarız:
- Her adımda, bir toplama işlemi gerektiren, terimlerin toplanmasının gerekli olduğu bir döngü (Yukarıdaki tek döngü örneklerindeki 1 + 2 + 3 + ... + n toplamı örneğini hatırlayalım.)
- Yukarda belirtilen döngünün her parametre değeri için, o adımdaki faktöriyeli hesaplatmak zorunda olduğumuz ve o nedenle yukarıdaki döngünün içinde yer alması gereken bir döngü.
KOD BLOĞU:
public class FaktoriyelliSeri
{
public static void main(String args[])
{
double s,fakt;
int i,j;
s=0;
for (i=2;i<=10;i++)
{
fakt=1;
for(j=1;j<=i;j++)
{
fakt=fakt*j;
}
s=s+1/fakt;
System.out.println(s);
}
System.out.println("Seri toplami "+s);
}
}
PROGRAMIN ÇIKTISI:
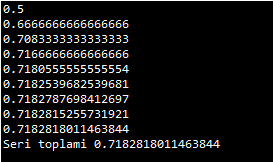
Programın çalıştırılması sonucu i, j, s ve fakt değişkenlerinin alacağı değerlerle ilgili tabloya göz atalım:
| DIŞ ÇEVRİM | İÇ ÇEVRİM | FAKTÖRİYEL | TOPLAM |
|---|---|---|---|
| i | j | fakt | s |
| 0 | |||
| 2 | 1 | 1 | 0 |
| 2 | 2 | 2 | 1/2 |
| 3 | 1 | 1 | 1/2 |
| 3 | 2 | 3 | 1/2 |
| 3 | 3 | 6(1.2.3=3!) | 1⁄2+1/6 |
| 4 | 1 | 1 | 1⁄2+1/6 |
| 4 | 2 | 2 | 1⁄2+1/6 |
| 4 | 3 | 6 | 1⁄2+1/6 |
| 4 | 4 | 24(1.2.3.4=4!) | 1⁄2+1/6+1/24 |
| ... | ... | ... | ... |
| 10 | 10 | 10! | 1⁄2+1/6+1/24+.. +1/20! |
SORU: Yukarıdaki seri toplamını, sadece bir for döngüsü kullanarak hesaplatabilir miyiz?
CEVAP: Evet. Yukarıdaki seri toplamını tek bir for döngüsü ile hesaplatan ve aynı sonuçları elde eden Java programının kod bloğu şöyledir:
public class FaktoriyelliSeri2
{
public static void main(String args[])
{
double s,fakt;
int i;
s=0;
fakt=1;
for (i=2; i<=10; i++)
{
fakt=fakt*i;
s=s+1/fakt;
System.out.println(s);
}
System.out.println("Seri toplami: "+s);
}
}
PROGRAMIN ÇIKTISI
