Algoritmaya Giriş

 

Algoritma, belirli bir işi yapmak için izlenen yol anlamındadır. Matematik ve bilgisayar programlamada sıkça kullanılır. Programlamaya başlamadan önce problemin çözümü bulunmalı ve çözüme giden yollar oluşturularak en verimli şekilde sonuçlandırılmalıdır. Çözüme giden bu yolların bulunması içinde sistematik düşüncenin geliştirilmesi gerekir. Algoritma oluşturulurken dikkat edilmesi gereken en önemli nokta, hesaplanabilir tüm olasılıkları ve onların çözüm yollarını bulabilmektir. Bir çözüm yolundaki tüm ayrımlar düşünülmeli ve bu ayrımlarda ne yapılacağı belirlenmelidir. Teorik olarak anlatıldığında anlaşılması zor bir kavram olan algoritmayı örneklerle açıklamaya çalışalım.

 

Örnek Durum:

İlk örneğimiz bilgisayarı çalıştırıp, gelecegiyazanlar portalına girmek olsun. Bunun için yapılması gereken ilk şey bilgisayarın açık olup olmadığı durumuna bakmaktır. Aşağıda çözümün akış diyagramını (flowchart) görmektesiniz.

Bilgisayar programlamada da benzer mantıkla algoritmalar oluşturulur. Önce çözüm yolları düşünülerek en makul çözüm bulunur. Ardından bu çözüm programlama dillerinden uygun olanları ile kodlanarak program, web sitesi, uygulama haline getirilir. Aşağıdaki örnek duruma bakıldığında bilgisayar mantığını biraz iyi daha anlayabiliriz. 

 

Örnek Durum:

Başlangıç ağırlıklarını bilmediğimiz 2 torbanın arasında bir ağırlık kontrolü yapalım. Torbalarımızdan biri X diğeri Y olsun. Bu torbaları karşılaştırıp karar vermeliyiz. Bunun için eşit kollu bir terazi kullanmamız gerekmektedir. Bu terazinin bir koluna X diğer koluna Y torbalarını yerleştirip sonucu gözlemleyebiliriz. Eğer ilk kol aşağıya inmişse X torbası daha ağırdır ya da ilk kol yukarıya çıkmışsa Y torbası daha ağırdır. Şimdi bunun programlamadaki yerine bakalım.

Burada X ve Y bizim değişkenlerimizdir, terazimiz ise bilgisayarımızdır. Terazinin kollarının verdiği tepkiler ise bilgisayarın bize verdiği cevaplardır.

Günümüz dünyasında bilgisayar programcılığı için en önemli şey, problemlere karşı üretilen algoritmalardır. Bir programcının algoritma kurma becerisi, onun yazacağı programların kalitesi ve optimizasyonu açısından çok önemlidir. Çünkü bu iki kavram, günümüz programcılığının en büyük handikaplarındandır.

Şimdi faktöriyel hesabının bilgisayar tarafından nasıl yapıldığını inceleyelim. Bilindiği üzere n!(n faktöriyel) ifadesi n*(n-1)*(n-2)*(n-3)...*2*1 ifadesine eşittir. Bu bilgiler ışığında kullanıcıdan alınan n sayısının faktöriyel hesabını bulalım.

 

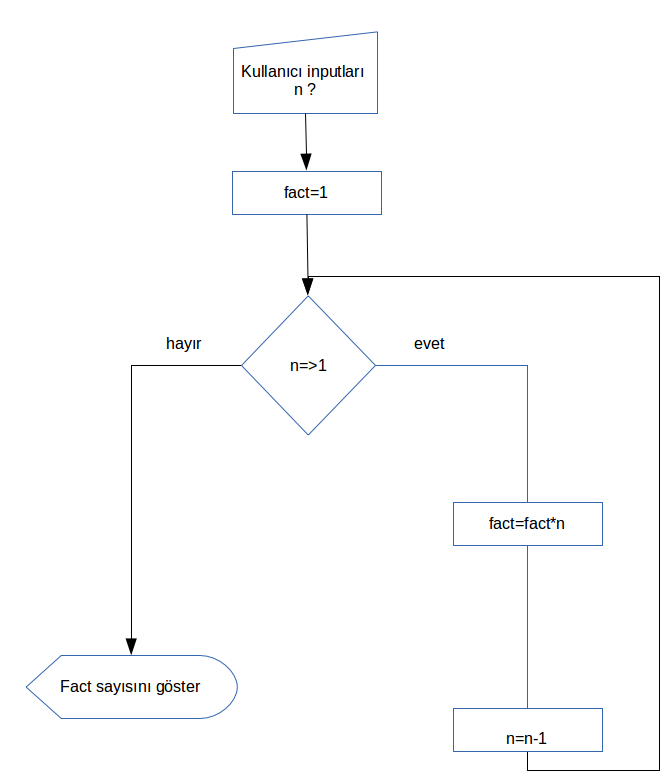
Örnek Durum:

Bu  örnek de fibonacci sayılarının hesabıyla ilgili olsun. Bunu yaparken dizileri kullanalım ki, çözümümüz her çağrıldığında işlemler tekrarlanmasın ve daha hızlı bir çözüm üretilebilsin. Fibonacci sayıları; kendisinden önceki iki sayının toplamına eşittir. Yani fibonacci serisi: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 ... şeklindedir. Şimdi kullanıcının bize n. fibonacci sayısını sorduğunu varsayalım.

Algoritmamız aşağıdaki gibi olacaktır.

Bu noktadan sonra örneklerimizin karmaşıklık seviyesini biraz daha arttıralım ve akış diyagramları yerine kod tasarımları ile devam edelim.

Örnek Durum:

Bilgisayar programcılığında kullanılan alan ve zaman arasında bir ters orantı vardır ve imkanlar sınırlıdır. Örneklemek gerekirse, yazacağınız bir uygulamada kullanıcının alacağı tepki süresinin uzun olmasını kabullenip, telefonun hafızasını daha az kullanmasını isteyebilirsiniz. Tabii ki bunun tam tersi de düşünülebilir. Fakat programın algoritması kurulurken gereksinimler ve sınırlamalar (alan ve tepki süresi gibi) göz önüne alınarak hazırlanmalı maksimum seviyede fayda kazanılmaya çalışmalıdır.

Anlatılanların daha iyi kavranılması için iki değişken ifadenin yerlerini değiştirme örneği üzerinden hareket edelim:

Problemimiz x=a , y=b ifadesini y=a , x=b şekline çevirmek olsun.

Alan kullanımının sınırsız olduğunun varsayıldığı çözüm şu şekilde olabilir:

x = a;
y = b;
temp = x; // x'in içindeki sayıyı kaybetmemek için boş bir alan yaratıp onu buraya kopyalıyoruz.
x = y; // x in kopyası olduğu için artık x'in üzerine y'yi yazabiliriz.
y = temp; // y değerinin üzerine temp değişkenini atayarak artık x=b, y=a çözümünü sağlamış olduk.

Aynı örneği alan sınırlaması olduğunu varsayarak yani fazladan alan kullanmadan çözelim:

x = a;
y = b;
x = x + y; // alanımızın sınırlı olduğunu varsayalım. x'i a+b ifadesine eşitleyelim.
y = x - y; // bu durumda y=a+b-b olacaktır.
x = x - y; // son olarak x=a+b-a olacak ve çözüme ulaşmış olacağız.

Örnek Durum:

Şimdi çok basit gibi gözüken fakat çözümü çok kolay olmayan başka bir örneğe geçelim. Örneğimiz, *'lar kullanarak bir eşkenar dörtgen çizdirmek olsun. Bunu belirli bir boyutta değil dinamik yapıda yapmak istiyoruz. Bunun için kullanıcıdan merkez satırınındaki karakter sayısını alalım. Algoritmamızda şu adımlar yer alacaktır:

• 
  
  input merkezsatırı; //kullanıcıdan merkez satırdaki * sayısı alınır.
  int satırsayısı = merkezsatırı*2-1;
  int satırdakiyıldızsayısı=1; //ilk satırımızda bir * şeklinde başlayacaktır.
  int satırdakiboşluksayısı = merkezsatırı - satırdakiyıldızsayısı
  while (satırsayısı>0) {
          while (satırdakiyıldızsayısı <= merkezsatırı) {
                  while (satırdakiboşluksayısı >= 0) {
                          print('' ''); //boşluk bastır
                  }
                  print(''x''); //x ve boşluk bastır
                  if (satırdakiyıldızsayısı < merkezsatırı)
                          satırdakiyıldızsayısı++ ;
                  else
                          satırdakiyıldızsayısı-- ;
                  }
          print(''\n''); //yeni satıra gecme
          satırsatırsayısı-- ;
          satirdakiboşluksayısı = merkezsatırı - satırdakiyıldızsayısı;
  }
  
  

   

  Kullanıcı merkez satırı 5 olarak belirlerse, çıkan şekil aşağıdaki gibi olacaktır.

      *
     * *
    * * *
  * * * *
  * * * * *
  * * * *
    * * *
     * *
      *